 И что бы мы делали без чисел? Хотя люди, которые не сильны в математике, предпочитают рассматривать любую информацию как текст, на практике большая часть информации в базах данных имеет числовую природу. Сколько единиц товара хранится на складе? Какую сумму мы задолжали? Насколько быстро развивается бизнес? Точные ответы на эти и многие другие вопросы можно получить именно в числовом выражении.
И что бы мы делали без чисел? Хотя люди, которые не сильны в математике, предпочитают рассматривать любую информацию как текст, на практике большая часть информации в базах данных имеет числовую природу. Сколько единиц товара хранится на складе? Какую сумму мы задолжали? Насколько быстро развивается бизнес? Точные ответы на эти и многие другие вопросы можно получить именно в числовом выражении.
Для работы с числами в PL/SQL необходимо хотя бы в общих чертах изучить:
- числовые типы данных, имеющиеся в вашем распоряжении (и в каких ситуациях их уместно применять);
- преобразование числовых значений в текст и обратно;
- богатую библиотеку встроенных функций PL/SQL.
Эти темы мы и начнем рассматривать в настоящей статье блога. Начнем с числовых типов данных языка PL/SQL.
Числовые типы данных PL/SQL
PL/SQL, как и РСУБД Oracle, поддерживает различные числовые типы данных для решения разных задач:
NUMBER— тип с фиксированной точностью, идеально подходящий для работы с денежными суммами. Это единственный из числовых типов PL/SQL, реализация которого совершенно не зависит от платформы. Все операции сNUMBERдолжны работать одинаково независимо от оборудования, на котором работает программа.PLS_INTEGERиBINARY_INTEGER— целочисленные типы, соответствующие представлению целых чисел на вашем оборудовании. Арифметические операции выполняются на уровне машинных команд. Значения этих типов не могут храниться в базе данных.SIMPLE_INTEGER— тип появился в Oracle Database 11g. Используется для представления значений из того же диапазона, что иBINARY_INTEGER, но не допускает хранениеNULLи не инициирует исключение при переполнении. Тип данныхSIMPLE_INTEGERсущественно ускоряет выполнение для кода, откомпилированного в машинный язык.BINARY_FLOATиBINARY_DOUBLE— двоичные типы с плавающей запятойIEEE-754одинарной и двойной точности. Я не рекомендую использовать эти типы для хранения денежных величин, но они могут пригодиться для быстрых вычислений с плавающей запятой.SIMPLE_FLOATиSIMPLE_DOUBLE— типы появились в Oracle Database 11g. Они поддерживают тот же диапазон, что иBINARY_FLOATcBINARY_DOUBLE, но не могут принимать значение NULL, не инициируют исключение при возникновении переполнения и не поддерживают специальные литералы и предикаты (такие, какBINARY_FLOAT_MIN_NORMAL,ISNANилиIS NOT INFINITE). Типы данныхSIMPLEсущественно ускоряют выполнение для кода, откомпилированного в машинный язык.
Возможно, вы также столкнетесь с другими числовыми типами — такими, как FLOAT, INTEGER и DECIMAL. Они представляют собой не что иное, как альтернативные имена для перечисленных мной основных числовых типов. Альтернативные имена более подробно рассматриваются в разделе «Числовые подтипы».
Тип NUMBER
Безусловно, самый распространенный числовой тип данных в мире Oracle и PL/SQL. Используется для хранения целых чисел, а также чисел с фиксированной или плавающей запятой практически любого размера. До выхода Oracle10g тип NUMBER был единственным числовым типом, непосредственно поддерживавшимся ядром баз данных Oracle (в последующих версиях также поддерживаются BINARY_FLOAT и BINARY_DOUBLE). Тип NUMBER имеет платформенно-независимую реализацию, а вычисления с типом NUMBER всегда приводят к одинаковому результату независимо от того, на какой аппаратной платформе выполняется программа.
В простейшем варианте переменная объявляется с ключевым словом NUMBER:
DECLARE x NUMBER;
Такое объявление определяет число с плавающей запятой. Память, выделяемая Oracle для переменной, позволяет хранить 40 значащих цифр, а плавающая десятичная запятая обеспечивает оптимальное представление присваиваемых значений. В переменных типа NUMBER могут храниться числа от 10−130 (1.0E — 130) до 10126 — 1 (1.0E126 — 1). Значения, меньшие 10−130, округляются до 0, а значения, большие либо равные 10126, считаются неопределенными; это создает проблемы на стадии выполнения, но не приводит к выдаче исключения. Диапазон значений NUMBER продемонстрирован в следующем блоке:
DECLARE
tiny_nbr NUMBER := 1e-130;
test_nbr NUMBER;
-- 1111111111222222222233333333334
-- 1234567890123456789012345678901234567890
big_nbr NUMBER := 9.999999999999999999999999999999999999999e125;
-- 1111111111222222222233333333334444444
-- 1234567890123456789012345678901234567890123456
fmt_nbr VARCHAR2(50) := '9.99999999999999999999999999999999999999999EEEE';
BEGIN
DBMS_OUTPUT.PUT_LINE('tiny_nbr =' || TO_CHAR(tiny_nbr, '9.9999EEEE'));
-- Слишком малые числа округляются до нуля
test_nbr := tiny_nbr / 1.0001;
DBMS_OUTPUT.PUT_LINE('tiny made smaller =' || TO_CHAR(test_nbr, fmt_nbr));
-- Слишком большие числа приводят к ошибке
DBMS_OUTPUT.PUT_LINE('big_nbr =' || TO_CHAR(big_nbr, fmt_nbr));
test_nbr := big_nbr * 1.0001; -- Слишком большое число
DBMS_OUTPUT.PUT_LINE('big made bigger =' || TO_CHAR(test_nbr, fmt_nbr));
END;
Результат выполнения программы:
tiny_nbr = 1.0000E-130
tiny made smaller = .00000000000000000000000000000000000000000E+00
big_nbr = 9.99999999999999999999999999999999999999900E+125
big made bigger =#################################################
При попытке явного присваивания переменной NUMBER слишком большого значения происходит исключение числового переполнения или потери значимости. Но в случае присваивания результата вычислений, превышающего самое большое допустимое значение, исключение не инициируется. Если приложению действительно необходимо работать с такими большими числами, придется либо организовать проверку диапазона, либо перейти на тип BINARY_DOUBLE, поддерживающий сравнение с BINARY_DOUBLE_INFINITY. С другой стороны, использование двоичных типов данных приводит к погрешностям округления. В большинстве приложений из-за ошибок округления предпочтение отдается типу NUMBER.
При объявлении переменной NUMBER можно задать для ее значения дополнительные параметры:
NUMBER (А, B)
Такое объявление определяет число с фиксированной запятой, где A — общее количество значащих цифр в числе, а B — количество цифр справа (положительное значение) или слева (отрицательное значение) от десятичной запятой. Оба параметра должны быть целочисленными литералами; ни переменные, ни константы в объявлении использоваться не могут. Допустимые значения параметра A находятся в диапазоне от 1 до 38, а параметра B — от –84 до 127.
При объявлении чисел с фиксированной запятой параметр B обычно меньше A. Например, переменную для хранения денежных сумм можно объявить как NUMBER(9,2); это позволяет представлять значения до 9 999 999,99 включительно. Интерпретация этого объявления показана на рис. 1.
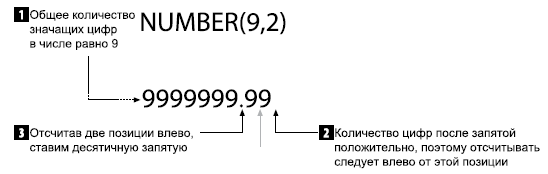
Рис. 1. Типичное объявление числа с фиксированной запятой
Как видно из рисунка, значение переменной NUMBER(9,2) представляет собой число с фиксированной запятой, состоящее из семи цифр слева от десятичной запятой и двух справа. Значения, хранимые в переменной, будут округляться максимум до сотых (табл. 1).
Попытка присваивания переменной двух последних значений вызывает исключение, поскольку для представления этих значений требуется больше цифр, чем помещается в переменной. Для хранения значений свыше 10 000 000 нужно минимум восемь значащих цифр в целой части числа. При округлении числа до семи цифр будут генерироваться ошибки. Ситуация становится более интересной при объявлении переменной, у которой количество цифр после десятичной запятой больше общего количества значащих цифр, или отрицательно. Пример представлен на рис. 2.
Переменная на рис. 2 содержит то же количество значащих цифр, что и переменная на рис. 1, но используются они по-другому. Поскольку параметр B равен 11, девять значащих цифр могут представлять только абсолютные значения меньше 0,01, которые округляются до стомиллиардных. Результаты присваивания некоторых значений переменной типа NUMBER(9,11) приведены в табл. 2.
| Исходное значение | Округленное значение |
| 1 234,56 | 1 234,56 |
| 1 234 567,984623 | 1 234 567,98 |
| 1 234 567,985623 | 1 234 567,99 |
| 1 234 567,995623 | 1 234 568,00 |
| 10 000 000,00 | Слишком большое значение — ошибка переполнения |
| –10 000 000,00 | То же |
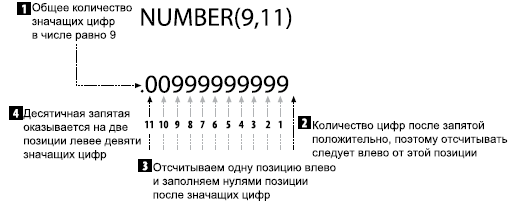
Рис. 2. Количество цифр после десятичной запятой больше
общего количества значащих цифр
| Исходное значение | Округленное значение |
| 0,00123456789 | 0,00123456789 |
| 0,000000000005 | 0,00000000001 |
| 0,000000000004 | 0,00000000000 |
| 0,01 | Слишком большое значение — ошибка переполнения |
| −0.01 | То же |
Если количество цифр в дробной части задано отрицательным значением, то десятичная запятая переносится вправо. Переменная, объявленная как NUMBER(9,-11), показана на рис. 3.
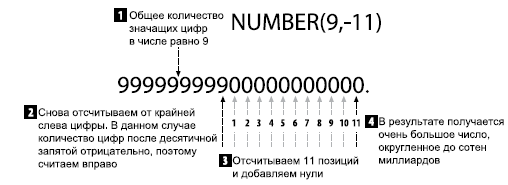
Рис. 3. Количество цифр после десятичной запятой задано отрицательным значением
Мы снова задали девять значащих цифр, но как видно из табл. 3, теперь вместо малых значений вплоть до стомиллиардных наименьшим значением, которое может содержаться в переменной, стало 100 миллиардов. Значения, меньшие 100 миллиардов, округляются вверх или вниз до ближайших 100 миллиардов, как видно из табл. 3.
| Исходное значение | Округленное значение |
| 50 000 000 000,123 | 100 000 000 000 |
| 49,999,999,999.999 | 0 |
| 150 000 975 230 001 | 150 000 000 000 000 |
| 100 000 000 000 000 000 000 или 1 × 1020 | Слишком большое значение — ошибка переполнения |
| −100 000 000 000 000 000 000 или -1 × 1020 | То же |
Как видно из рис. 3 и табл. 3, отрицательное значение параметра, определяющего количество цифр после запятой, позволяет представлять очень большие значения — но за счет потери данных в младших разрядах. При записи в переменную, объявленную как NUMBER(9,-11), любое абсолютное значение меньше 50 триллионов округляется до нуля.
Учтите, что при объявлении переменных типа NUMBER количество цифр после десятичной запятой не является обязательным параметром и по умолчанию равняется нулю. Например, следующие два объявления эквивалентны:
x NUMBER(9,0); x NUMBER(9);
Оба объявления создают целочисленную переменную (то есть переменную с нулем цифр в дробной части) из девяти значащих цифр. В такой переменной могут храниться числа из диапазона от −999 999 999 до 999 999 999.
При использовании с дробными значениями диапазон NUMBER ограничивается параметрами, как продемонстрировано в следующем программном блоке:
DECLARE
low_nbr NUMBER(38,127);
high_nbr NUMBER(38,-84);
BEGIN
/* 127 - наибольшее значение второго параметра, поэтому начинаем
с 1 и перемещаем запятую на 127 позиций влево. Все просто. */
low_nbr := 1E-127;
DBMS_OUTPUT.PUT_LINE('low_nbr = ' || low_nbr);
/* −84 - наиименьшее значение второго параметра. Прибавляем
37 для нормализации научной записи, получаем E+121. */
high_nbr := 9.9999999999999999999999999999999999999E+121;
DBMS_OUTPUT.PUT_LINE('high_nbr = ' || high_nbr);
END;
Результат:
low_nbr =
1.000000000000000000000000000000000000000000000000000000000000000000000000000000
000000000000000E-127
high_nbr =
9.999999999999999999999999999999999999900000000000000000000000000000000000000000
000000000000000E+121
Как и прежде, low_nbr представляет нижнюю, а high_nbr — верхнюю границу положительного диапазона. Обратите внимание: при работе с числами с фиксированной запятой точность ограничивается 38 значащими цифрами.
При таком широком диапазоне допустимых значений и разнообразных возможностях не удивительно, что тип данных NUMBER столь популярен. Используя в объявлениях только ключевое слово NUMBER, можно создать переменные с плавающей запятой, а задавая параметры — переменные с фиксированной запятой. Если количество цифр после запятой указать равным нулю или не задавать вовсе, получится целочисленная переменная. Таким образом, один тип данных NUMBER покрывает все возможные варианты числовых значений.
Тип PLS_INTEGER
Тип данных PLS_INTEGER позволяет хранить целые числа в диапазоне от −2 147 483 648 до 2 147 483 647. Значения хранятся в «родном» целочисленном формате аппаратной платформы. Несколько примеров объявлений переменных типа PLS_INTEGER:
DECLARE loop_counter PLS_INTEGER; days_in_standard_year CONSTANT PLS_INTEGER := 365; emp_vacation_days PLS_INTEGER DEFAULT 14;
Тип данных PLS_INTEGER был разработан для увеличения скорости вычислений. До выхода Oracle10g тип PLS_INTEGER был единственным целочисленным типом, использовавшим машинные вычисления. Все остальные типы данных использовали математическую библиотеку языка C. В результате операции со значениями типа PLS_INTEGER выполняются быстрее операций со значениями NUMBER. А поскольку значения PLS_INTEGER целочисленные, проблем совместимости при переходе с одной платформы на другую из-за них практически не бывает.
Используйте PLS_INTEGER, если ваша программа интенсивно выполняет целочисленные операции. Однако следует помнить, что в выражениях, где приходится выполнять частые преобразования к типу NUMBER и обратно, лучше изначально использовать тип NUMBER. Наибольшая эффективность достигается при использовании PLS_INTEGER для целочисленной арифметики (и счетчиков циклов) там, где удается избежать многочисленных преобразований к типу NUMBER и обратно. Как показывает следующий пример, при использовании этого типа в целочисленной арифметике полученные значения округляются до целых чисел:
DECLARE
int1 PLS_INTEGER;
int2 PLS_INTEGER;
int3 PLS_INTEGER;
nbr NUMBER;
BEGIN
int1 := 100;
int2 := 49;
int3 := int2/int1;
nbr := int2/int1;
DBMS_OUTPUT.PUT_LINE('integer 100/49 =' || TO_CHAR(int3));
DBMS_OUTPUT.PUT_LINE('number 100/49 =' || TO_CHAR(nbr));
int2 := 50;
int3 := int2/int1;
nbr := int2/int1;
DBMS_OUTPUT.PUT_LINE('integer 100/50 =' || TO_CHAR(int3));
DBMS_OUTPUT.PUT_LINE('number 100/50 =' || TO_CHAR(nbr));
END;
Программа выводит следующий результат:
integer 100/49 =0 number 100/49 =.49 integer 100/50 =1 number 100/50 =.5
Если итоговое значение целочисленной операции выходит за пределы диапазона допустимых значений (от −2 147 483 648 до 2 147 483 647), произойдет ошибка целочисленного переполнения.
Тип BINARY_INTEGER
Тип данных BINARY_INTEGER позволяет хранить целые числа со знаком в двоичном формате. Семантика этого типа данных изменилась в Oracle10g Release 1. Начиная с этой версии тип BINARY_INTEGER стал эквивалентным PLS_INTEGER. В Oracle9i Release 2 и более ранних версиях тип BINARY_INTEGER отличался от PLS_INTEGER тем, что он был реализован с использованием платформенно-независимого библиотечного кода.
Любопытная подробность: казалось бы, в пакете STANDARD тип BINARY_INTEGER ограничивается значениями от −2 147 483 647 до 2 147 483 647, однако в моей программе не инициировались исключения при присваивании значений из диапазона от −2 147 483 648 до 2 147 483 647 (немного расширенного в отрицательной части):
subtype BINARY_INTEGER is INTEGER range '-2147483647'..2147483647;
Тип BINARY_INTEGER не рекомендуется использовать в новых разработках — разве что вам потребуется, чтобы код работал в старых версиях Oracle до 7.3 (версия, в которой появился тип PLS_INTEGER). Надеюсь, вам не приходится иметь дела с такими древностями!
Тип SIMPLE_INTEGER
Тип SIMPLE_INTEGER появился в Oracle11g. Он представляет собой оптимизированную по быстродействию версию PLS_INTEGER с некоторыми ограничениями. Тип SIMPLE_INTEGER имеет такой же диапазон значений, как PLS_INTEGER (от −2 147 483 648 до 2 147 483 647), но не поддерживает NULL и не проверяет условия переполнения. Казалось бы, зачем использовать этот неполноценный дубликат PLS_INTEGER? Если ваша программа компилируется в машинный код, а ситуация такова, что NULL и переполнение исключены, тип SIMPLE_INTEGER обеспечит значительно лучшее быстродействие. Рассмотрим следующий пример:
/* Файл в Сети: simple_integer_demo.sql */ -- Начнем с создания процедуры, требующей большого объема -- вычислений, с использованием PLS_INTEGER CREATE OR REPLACE PROCEDURE pls_test (iterations IN PLS_INTEGER) AS int1 PLS_INTEGER := 1; int2 PLS_INTEGER := 2; begints timestamp; endts timestamp; BEGIN begints := SYSTIMESTAMP; FOR cnt IN 1 .. iterations LOOP int1 := int1 + int2 * cnt; END LOOP; endts := SYSTIMESTAMP; DBMS_OUTPUT.put_line( iterations || ' итераций за время:' || TO_CHAR (endts - begints)); END; / -- Затем та же процедура создается с использованием SIMPLE_INTEGER CREATE OR REPLACE PROCEDURE simple_test (iterations IN SIMPLE_INTEGER) AS int1 SIMPLE_INTEGER := 1; int2 SIMPLE_INTEGER := 2; begints timestamp; endts timestamp; BEGIN begints := SYSTIMESTAMP; FOR cnt IN 1 .. iterations LOOP int1 := int1 + int2 * cnt; END LOOP; endts := SYSTIMESTAMP; DBMS_OUTPUT.put_line( iterations || ' итераций за время:' || TO_CHAR (endts - begints)); END; / -- Сначала процедуры перекомпилируются в режиме интерпретации ALTER PROCEDURE pls_test COMPILE PLSQL_CODE_TYPE=INTERPRETED; / ALTER PROCEDURE simple_test COMPILE PLSQL_CODE_TYPE=INTERPRETED / -- Сравнить время выполнения BEGIN pls_test(123456789); END; / 123456789 итераций за время:+000000000 00:00:06.375000000 BEGIN simple_test(123456789); END; / 123456789 итераций за время:+000000000 00:00:06.000000000 -- Перекомпиляция в машинный код ALTER PROCEDURE pls_test COMPILE PLSQL_CODE_TYPE=NATIVE / ALTER PROCEDURE simple_test COMPILE PLSQL_CODE_TYPE= NATIVE / -- Сравнение времени выполнения BEGIN pls_test(123456789); END; / 123456789 итераций за время:+000000000 00:00:03.703000000 BEGIN simple_test(123456789); END; / 123456789 итераций за время:+000000000 00:00:01.203000000
Из этого примера видно, что тип SIMPLE_INTEGER обеспечивает небольшое преимущество по быстродействию интерпретируемого кода (6% в тесте на сервере Microsoft Windows). Оба типа, PLS_INTEGER и SIMPLE_INTEGER быстрее работают при компиляции в машинный код, но в «машинном» варианте SIMPLE_INTEGER, работает на 300% быстрее, чем PLS_INTEGER! В качестве упражнения проведите этот тест с типом NUMBER — я обнаружил, что SIMPLE_INTEGER превосходит NUMBER по производительности на 1000%. На сервере Linux с Oracle Database 11g Release 2 аналогичные различия в производительности наблюдались при использовании SIMPLE_INTEGER (часто на несколько сотен процентов быстрее, чем с альтернативными числовыми типами).
Типы BINARY_FLOAT и BINARY_DOUBLE
В Oracle10g появились два новых вещественных типа: BINARY_FLOAT и BINARY_DOUBLE. Они соответствуют вещественным типам с одинарной и двойной точностью, определенным в стандарте IEEE-754. Эти типы реализуются как PL/SQL, так и самим ядром базы данных, поэтому они могут использоваться и в определениях таблиц, и в коде PL/SQL.
В табл. 4 эти новые типы сравниваются с популярным типом NUMBER.
| Характеристика | BINARY_FLOAT | BINARY_DOUBLE | NUMBER |
| Максимальное абсолютное значение | 3,40282347E+38F | 1,7976931348623157E+308 | 9.999...999E+121 (38 «девяток») |
| Минимальное абсолютное значение | 1.17549435E–38F | 2.2250748585072014E−308 | 1.0E–127 |
| Количество байтов, используемое для значения | 4 (32 бита) | 8 (64 бита) | от 1 до 20 |
| Количество байтов длины | 0 | 0 | 1 |
| Представление | Двоичное, IEEE-754 | Двоичное, IEEE-754 | Десятичное |
| Суффикс литералов | f | d | Нет |
При записи литералов этих новых типов добавляется суффикс f или d — в зависимости от того, должен ли литерал интерпретироваться как BINARY_FLOAT или BINARY_DOUBLE.
Пример:
DECLARE my_binary_float BINARY_FLOAT := .95f; my_binary_double BINARY_DOUBLE := .95d; my_number NUMBER := .95;
Также существуют специальные литералы, используемые при работе с вещественными типами IEEE-754. Следующие литералы поддерживаются как в PL/SQL, так и в SQL:
BINARY_FLOAT_NANиBINARY_DOUBLE_NAN— «не число» одинарной или двойной точности соответственно.BINARY_FLOAT_INFINITYиBINARY_DOUBLE_INFINITY— бесконечность одинарной или двойной точности соответственно.
Другая группа литералов поддерживается только в PL/SQL:
BINARY_FLOAT_MIN_NORMAL,BINARY_FLOAT_MAX_NORMAL— границы нормального диапазона значений для переменных с одинарной и двойной точностью соответственно.BINARY_FLOAT_MIN_SUBNORMAL,BINARY_DOUBLE_MIN_SUBNORMAL— границы субнормального диапазона значений — части стандарта IEEE-754, предназначенной для снижения риска, связанного с потерей значимости.
Наконец, при работе с этими типами данных используются следующие предикаты:
IS NANиIS NOT NAN— проверяет, является ли значение IEEE-754 «не числом».IS INFINITEиIS NOT INFINITE— проверяет, представляет ли значение IEEE-754 бесконечность.
Очень важно помнить, что типы BINARY являются двоичными. Их не рекомендуется использовать ни в каких ситуациях, требующих точного десятичного представления. Следующий пример показывает, почему эти типы не должны, например, использоваться для представления денежных сумм:
BEGIN DBMS_OUTPUT.PUT_LINE(0.95f); --BINARY_FLOAT DBMS_OUTPUT.PUT_LINE(0.95d); --BINARY_DOUBLE DBMS_OUTPUT.PUT_LINE(0.95); --NUMBER END; Программа выводит следующий результат: 49999988E-001 4999999999999996E-001 .95
По аналогии с тем, как некоторые дроби (например, 1/3) невозможно точно представить в виде десятичного числа, в некоторых случаях десятичные числа — как, например, 0,95 — не имеют точного представления в двоичном виде. При работе с денежными суммами следует использовать тип NUMBER.
Будьте внимательны при смешении вещественных типов при сравнениях, например:
BEGIN
IF 0.95f = 0.95d
THEN
DBMS_OUTPUT.PUT_LINE('TRUE');
ELSE
DBMS_OUTPUT.PUT_LINE('FALSE');
END IF;
IF ABS(0.95f - 0.95d) < 0.000001d
THEN
DBMS_OUTPUT.PUT_LINE('TRUE');
ELSE
DBMS_OUTPUT.PUT_LINE('FALSE');
END IF;
END; Программа выводит следующий результат:
FALSE TRUE
Вывод FALSE и TRUE соответственно демонстрирует коварные проблемы, с которыми можно столкнуться при представлении десятичных значений в двоичной форме. Представление 0,95 в формате BINARY_DOUBLE содержит больше цифр, чем версия BINARY_FLOAT, поэтому эти два значения при сравнении не считаются равными. Второе сравнение дает результат TRUE; чтобы компенсировать невозможность точного представления 0,95 в двоичной форме, мы произвольно решаем, что два значения считаются равными, если разность между ними меньше одной миллионной.
Для чего используются типы IEEE-754? Первая причина — производительность, вторая — соответствие стандартам IEEE. При выполнении масштабных вычислений использование типов IEEE-754 может привести к заметному выигрышу по скорости. Следующий программный блок выводит время, необходимое для вычисления площади 5 000 000 кругов и вычисления 5 000 000 синусов. Обе задачи выполняются дважды — с BINARY_DOUBLE и NUMBER:
/* Файл в Сети: binary_performance.sql */
DECLARE
bd BINARY_DOUBLE;
bd_area BINARY_DOUBLE;
bd_sine BINARY_DOUBLE;
nm NUMBER;
nm_area NUMBER;
nm_sine NUMBER;
pi_bd BINARY_DOUBLE := 3.1415926536d;
pi_nm NUMBER := 3.1415926536;
bd_begin TIMESTAMP(9);
bd_end TIMESTAMP(9);
bd_wall_time INTERVAL DAY TO SECOND(9);
nm_begin TIMESTAMP(9);
nm_end TIMESTAMP(9);
nm_wall_time INTERVAL DAY TO SECOND(9);
BEGIN
-- Площадь круга вычисляется 5 000 000 раз с BINARY_DOUBLE
bd_begin := SYSTIMESTAMP;
bd := 1d;
LOOP
bd_area := bd * bd * pi_bd;
bd := bd + 1d;
EXIT WHEN bd > 5000000;
END LOOP;
bd_end := SYSTIMESTAMP;
-- Площадь круга вычисляется 5 000 000 раз с NUMBER
nm_begin := SYSTIMESTAMP;
nm := 1;
LOOP
nm_area := nm * nm * 2 * pi_nm;
nm := nm + 1;
EXIT WHEN nm > 5000000;
END LOOP;
nm_end := SYSTIMESTAMP;
-- Вычисление и вывод затраченного времени
bd_wall_time := bd_end - bd_begin;
nm_wall_time := nm_end - nm_begin;
DBMS_OUTPUT.PUT_LINE('BINARY_DOUBLE area = ' || bd_wall_time);
DBMS_OUTPUT.PUT_LINE('NUMBER area = ' || nm_wall_time);
-- Синус вычисляется 5 000 000 раз с BINARY_DOUBLE
bd_begin := SYSTIMESTAMP;
bd := 1d;
LOOP
bd_sine := sin(bd);
bd := bd + 1d;
EXIT WHEN bd > 5000000;
END LOOP;
bd_end := SYSTIMESTAMP;
-- Синус вычисляется 5 000 000 раз с NUMBER
nm_begin := SYSTIMESTAMP;
nm := 1;
LOOP
nm_sine := sin(nm);
nm := nm + 1;
EXIT WHEN nm > 5000000;
END LOOP;
nm_end := SYSTIMESTAMP;
-- Вычисление и вывод затраченного времени
bd_wall_time := bd_end - bd_begin;
nm_wall_time := nm_end - nm_begin;
DBMS_OUTPUT.PUT_LINE('BINARY_DOUBLE sine = ' || bd_wall_time);
DBMS_OUTPUT.PUT_LINE('NUMBER sine = ' || nm_wall_time);
END;
Мои результаты, которые получились довольно стабильными для серии запусков, выглядели так:
BINARY_DOUBLE area = +00 00:00:02.792692000 NUMBER area = +00 00:00:08.942327000 BINARY_DOUBLE sine = +00 00:00:04.149930000 NUMBER sine = +00 00:07:37.596783000
Но не надо слишком доверять тестам — в том числе и тем, которые я только что привел! Как видно из примера, диапазон возможного прироста производительности от использования типа IEEE-754 вместо NUMBER весьма велик. При использовании BINARY_DOUBLE вычисление площади круга 5 миллионов раз занимает приблизительно 40% времени от его вычисления с использованием NUMBER. Однако при вычислении синуса 5 миллионов раз задача решается всего за 0,9% времени. В каждой конкретной ситуации выигрыш зависит от используемых вычислений. Из всего сказанного не стоит делать вывод, что типы IEEE-754 позволят выполнить работу на фиксированные X% быстрее, чем NUMBER. Скорее речь идет о том, что потенциальный прирост производительности от использования типов IEEE-754 вместо NUMBER может быть заметным и его стоит принять во внимание при выполнении масштабных вычислений.
Смешанное использование типов с плавающей запятой
Oracle устанавливает систему приоритетов для неявных преобразований типов с плавающей запятой. В порядке убывания приоритетов типы образуют последовательность BINARY_DOUBLE, BINARY_FLOAT и NUMBER. Когда вы пишете выражение, в котором используется комбинация этих типов, база данных пытается преобразовать все значения к наивысшему приоритету из выражения. Например, если в выражении используются BINARY_FLOAT и NUMBER, Oracle сначала преобразует все значения к типу BINARY_FLOAT.
Если вы не хотите, чтобы база данных выполняла эти неявные преобразования, используйте функции TO_NUMBER, TO_BINARY_FLOAT и TO_BINARY_DOUBLE:
DECLARE nbr NUMBER := 0.95; bf BINARY_FLOAT := 2; nbr1 NUMBER; nbr2 NUMBER; BEGIN -- Приоритет по умолчанию, повысить до binary_float nbr1 := nbr * bf; -- Понизить BINARY_FLOAT до NUMBER nbr2 := nbr * TO_NUMBER(bf); DBMS_OUTPUT.PUT_LINE(nbr1); DBMS_OUTPUT.PUT_LINE(nbr2); END; Результат выглядит так: 1.89999998 1.9
Чтобы избежать неоднозначности и возможных ошибок с неявными преобразованиями, я рекомендую применять явные преобразования — например, с применением функций TO_NUMBER, TO_BINARY_FLOAT и TO_BINARY_DOUBLE.
Впрочем, в некоторых областях реализация двоичных вещественных типов Oracle не полностью соответствует стандарту IEEE-754. Например, Oracle преобразует −0 в +0, тогда как стандарт IEEE-754 такого поведения не требует. Если совместимость со стандартом важна для вашего приложения, обратитесь к разделу «Типы данных» руководства SQL Reference от Oracle — в нем содержится точная информация о том, где и как Oracle отклоняется от стандарта IEEE-754.
Типы SIMPLE_FLOAT и SIMPLE_DOUBLE
Типы данных SIMPLE_FLOAT и SIMPLE_DOUBLE появились в Oracle11g. Они представляют собой оптимизированные по быстродействию версии BINARY_FLOAT и BINARY_DOUBLE с некоторыми ограничениями. Типы SIMPLE_FLOAT и SIMPLE_DOUBLE имеют такие же диапазоны значений, как BINARY_FLOAT и BINARY_DOUBLE, но не поддерживают значения NULL, специальные литералы IEEE (BINARY_FLOAT_NAN, BINARY_DOUBLE_INFINITY и т. д.), специальные предикаты IEEE (IS NAN, IS INFINITY и т. д.). Кроме того, они не проверяют условие переполнения. Как и тип SIMPLE_INTEGER, эти специализированные типы в соответствующей ситуации способны значительно ускорить выполнение кода.
Числовые подтипы
Oracle также поддерживает ряд числовых подтипов данных. Большая их часть представляет собой альтернативные имена для трех описанных нами базовых типов данных.
Подтипы введены для достижения совместимости с типами данных ISO SQL, SQL/DS и DB2 и обычно имеют те же диапазоны допустимых значений, что и их базовые типы. Однако иногда значения подтипа ограничены некоторым подмножеством значений базового типа. Подтипы числовых данных представлены в табл. 5.
| Подтип | Совместимость | Соответствующий тип данных Oracle |
| DEC (A, B) | ANSI | NUMBER (A,B) |
| DECIMAL (A, B) | IBM | NUMBER (A,B) |
| DOUBLE PRECISION | ANSI | NUMBER, точность 126 двоичных цифр |
| FLOAT | ANSI, IBM | NUMBER, точность 126 двоичных цифр |
| FLOAT (двоичная_точность) | ANSI, IBM | NUMBER, с точностью до 126 двоичных цифр(по умолчанию) |
| INT | ANSI | NUMBER(38) |
| INTEGER | ANSI, IBM | NUMBER(38) |
| NATURAL | N/A | PLS_INTEGER*, но только с неотрицательными значениями (0 и выше) |
| NATURALN | N/A | То же, что NATURAL, но с запретом NULL |
| NUMERIC (A, B) | ANSI | NUMBER (A,B) |
| POSITIVE | N/A | PLS_INTEGER*, но только с положительными значениями (1 и выше) |
| POSITIVEN | N/A | То же, что POSITIVE, но с запретом NULL |
| REAL | ANSI | NUMBER, точность 63 цифры |
| SIGNTYPE | N/A | PLS_INTEGER* с возможными значениями –1, 0 и 1 |
| SMALLINT | ANSI, IBM | NUMBER (38) |
* BINARY_INTEGER до Oracle10g.
Типы данных NUMERIC, DECIMAL и DEC позволяют объявлять только значения с фиксированной запятой. Типы DOUBLE PRECISION и REAL эквивалентны NUMBER. С помощью типа FLOAT можно объявлять числа с плавающей запятой с двойной точностью в диапазоне от 63 до 126 бит. Возможность определения точности числа в битах, а не в цифрах неудобна, и, скорее всего, вам не придется использовать типы данных ISO/IBM. На практике часто используются подтипы PLS_INTEGER, к которым относятся NATURAL и POSITIVE. Они ограничивают значения, которые могут храниться в переменной, а их применение делает логику программы более понятной. Например, если переменная может принимать только неотрицательные значения, ее можно объявить с типом NATURAL (0 и выше) или POSITIVE (1 и выше). Такое объявление будет способствовать самодокументированию кода.

