Let us consider a neuron i as shown in Fig. 1.2, which receives inputs from axons that we label j through synapses of strength wij . The first subscript (i) refers to the output neuron that receives synaptic inputs, and the second subscript (j) to the particular input. j counts from 1 to C , where C is the number of synapses or connections received. The firing rate of the ith neuron is denoted as yi, and that of the jth input to the neuron as xj . To express the idea that the neuron makes a simple linear summation of the inputs it receives, we can write the activation of neuron i, denoted hi , as where j indicates that the sum is over the C input axons (or connections) indexed by j to each neuron.
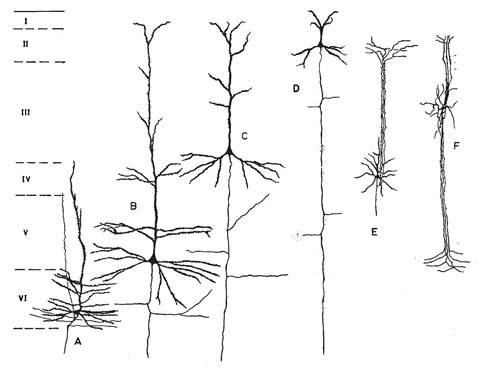
Fig. 1.2. Notation used to describe an individual neuron in a network model. By convention, we generally represent the dendrite as thick, and vertically oriented (as this is the normal way that neuroscientists view cortical pyramidal cells under the microscope); and the axon as thin. The cell body or soma is indicated between them by the triangle, as many cortical neurons have a pyramidal shape. The firing rate we also call the activity of the neuron.

The multiplicative form here indicates that activation should be produced by an axon only if it is firing, and depending on the strength of the synapse wij from input axon j onto the dendrite of the receiving neuron i. Equation 1.1 indicates that the strength of the activation reflects how fast the axon j is firing (that is xj ), and how strong the synapse wij is. The sum of all such activations expresses the idea that summation (of synaptic currents in real neurons) occurs along the length of the dendrite, to produce activation at the cell body, where the activation hi is converted into firing yi. This conversion can be expressed as which indicates that the firing rate is a function (f) of the postsynaptic activation.
yi = f(hi) (1.2)
The function at its simplest could be linear, so that the firing rate would be proportional to the activation (see Fig. 1.3a). Real neurons have thresholds, with firing occurring only if the activation is above the threshold. A threshold linear activation function is shown in Fig. 1.3b. This has been useful in formal analysis of the properties of neural networks. Neurons also have firing rates that become saturated at a maximum rate, and we could express this as the sigmoid activation function shown in Fig. 1.3c. Another simple activation function, used in some models of neural networks, is the binary threshold function (Fig. 1.3d), which indicates that if the activation is below threshold, there is no firing, and that if the activation is above threshold, the neuron fires maximally. Some non-linearity in the activation function is an advantage, for it enables many useful computations to be performed in neuronal networks, including removing interfering effects of similar memories, and enabling neurons to perform logical operations, such as firing only if several inputs are present simultaneously.
A property implied by equation 1 is that the postsynaptic membrane is electrically short, and so summates its inputs irrespective of where on the dendrite the input is received. In real neurons, the transduction of current into firing frequency (the analogue of the transfer
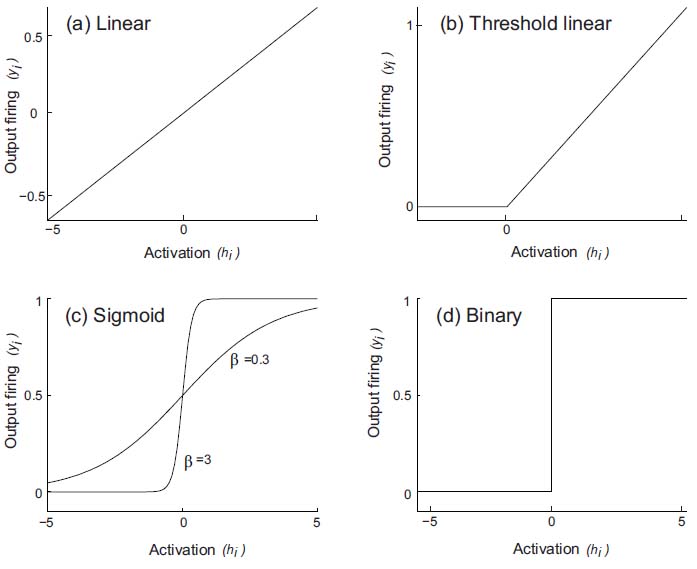
Fig. 1.3 Different types of activation function. The activation function relates the output activity (or firing rate), yi , of the neuron (i) to its activation, hi. (a) Linear. (b) Threshold linear. (c) Sigmoid. [One mathematical exemplar of this class of activation function is yi = 1/(1 + exp(−2βhi)). The output of this function, also sometimes known as the logistic function, is 0 for an input of — ∞, 0.5 for 0, and 1 for +∞. The function incorporates a threshold at the lower end, followed by a linear portion, and then an asymptotic approach to the maximum value at the top end of the function. The parameter в controls the steepness of the almost linear part of the function round hi = 0. If в is small, the output goes smoothly and slowly from 0 to 1 as hi goes from — ∞ to +∞. If в is large, the curve is very steep, and approximates a binary threshold activation function. (d) Binary threshold.
function of equation 1.2) is generally studied not with synaptic inputs but by applying a steady current through an electrode into the soma. Examples of the resulting curves, which illustrate the additional phenomenon of firing rate adaptation, are shown in Fig. 1.4.
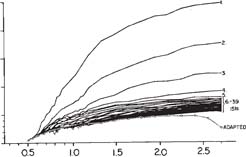
Fig. 1.4 Activation function of a hippocampal CA1 neuron. Frequency - current plot (the closest experimental analogue of the activation function) for a CA1 pyramidal cell. The firing frequency (in Hz) in response to the injection of 1.5 s long, rectangular depolarizing current pulses has been plotted against the strength of the current pulses (in nA) (abscissa). The first 39 interspike intervals (ISIs) are plotted as instantaneous frequency (1 / ISI), together with the average frequency of the adapted firing during the last part of the current injection (circles and broken line). The plot indicates a current threshold at approximately 0.5 nA, a linear range with a tendency to saturate, for the initial instantaneous rate, above approximately 200 Hz, and the phenomenon of adaptation, which is not reproduced in simple non-dynamical models (see further Appendix A5 of Rolls and Treves 1998). (Reproduced from Lanthorn, T., Storm, J. and Andersen, P. (1984) Current-to-frequency transduction in CA1 hippocampal pyramidal cells: Slow prepotentials dominate the primary range firing. Experimental Brain Research 53: 431-443, Copyright © Springer-Verlag.)



